En las ecuaciones trigonométricas intervienen funciones trigonométricas, que son periódicas y por tanto sus soluciones se pueden presentar en uno o en dos cuadrantes y además se repiten en todas las vueltas.
Para resolver una ecuación trigonométrica haremos las transformaciones necesarias para trabajar con una sola función trigonométrica, para ello utilizaremos las identidades trigonométricas fundamentales.



















 TRIANGULO RECTÁNGULO ISÓSCELES
TRIANGULO RECTÁNGULO ISÓSCELES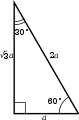 TRIANGULO RECTÁNGULO ESCALENO
TRIANGULO RECTÁNGULO ESCALENO
